Hydrogen
Ion Concentration in Acid Solutions
Acid dissociation constants are used to calculate the hydrogen ion concentration
in the solution of an acid.
A. Hydrogen Ion Concentration in Solutions
of Strong Acids
Strong acids with one ionizable hydrogen are completely ionized in aqueous solution;
therefore, the hydrogen ion concentration of these solutions is equal to the
molar concentration of the acid.
|
Example:
What is the hydrogen ion concentration in 1.0 M HCl?
Solution
Hydrochloric acid is a strong acid that is completely ionized in water.
HCl  H+ +
Cl- H+ +
Cl-
Therefore, in a solution prepared by adding 1.0 mol HCl to enough water
to make 1.0 L solution, the concentration of H+ is 1.0 M, that of Cl-
is 1.0 M and that of undissociated acid is 0.
|
B. Hydrogen Ion Concentration in Solutions
of Weak Acids
The hydrogen ion concentration of an aqueous solution of a weak acid depends
on the value of its acid dissociation constant and is always less than the concentration
of the weak acid. The hydrogen ion concentration can be calculated using the
value of Ka and the molar concentration of the weak acid.
Acetic acid is a weak acid that ionizes according to the equation
HC2H3O2 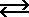 H+ + C2H3O2-
H+ + C2H3O2-
Its acid dissociation constant is
| |
Ka = |
[H+][C2H3O2-]
[HC2H3O2] |
= 1.8 X 10-5 |
The hydrogen ion concentration of a 1.0 M acetic acid solution can be calculated
as follows: The solution contains 1.0 mol acetic acid in 1.0 L solution. Because
acetic acid is a weak electrolyte, only a small fraction of the molecules ionize
to hydrogen and acetate ions; most remain as un-ionized acetic acid molecules.
Let x stand for the number of moles of acetic acid that ionize. If x moles ionize,
then 1.0 - x moles of acetic acid remain un-ionized. For x moles of acetic acid
that ionize, x moles of H+ and x moles of C2H3O2-
are formed. The resulting concentrations of acetic acid, hydrogen ion, and acetate
ion at equilibrium are
| |
HC2H3O2
1.0 - x |
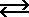
|
H+
x |
+
|
C2H3O2-
x |
Substituting these values into the expression for the acid dissociation constant
gives:
| |
Ka = |
[H+][C2H3O2-]
[HC2H3O2] |
= |
(x)(x)
1.0 - x |
= 1.8 X 10-5 |
The tiny value of the acid dissociation constant suggests that the amount
of acid dissociated is very small (less than 0.01 M). Using the rules for significant
figures in addition and subtraction Section 2.2C), we know that the quantity
1.0 - 0.01 expressed to two significant figures is 1.0. If x has a value less
than 0.01, it is appropriate to disregard x in the expression 1.0 - x and change
the Ka expression to:
| |
Ka = |
x2
1.0 |
�
= 1.8 X 10-5 |
Solving this equation gives:
x2 = 1.8 X 10-5 = 18 X 10-6
x = 4.2 X 10-3 = [H+] = [C2H3O2-]
These values are shown in Table 12.5.
TABLE 12.5 Concentrations of species in 1.0 M acetic acid
solution
| |
In calculation |
Calculated value |
| acetic acid molecules |
1.0 - x |
1.0 M |
| hydrogen ions |
x |
4.2 X 10-3 M |
| acetate ions |
x |
4.2 X 10-3 M |
The hydrogen ion concentration in 1.0 M acetic solution is, then, 4.2 X 10-3
M, or 0.0042 M. The number 0.0042 is not significant when subtracted from 1.0,
so our simplification of the original equation was justified. If the acid is
very dilute, for example 10-3 M, or if it is one with a large dissociation
constant, such as 10-2, this simplification would not be valid. These
calculations emphasize the difference between strong and weak acids. The hydrogen
ion concentration of a 1.0 M solution of a strong acid is 1.0 M (see Example
12.7). The hydrogen ion concentration of a 1.0 M solution of a weak acid can
be calculated from the acid dissociation constant of the weak acid and is much
less than 1.0 M.
|
Example:
Calculate the hydrogen ion concentration in 0.10 M ascorbic acid, C6H8O6,
a weak acid. the Ka for ascorbic acid is 8.0x10-5.
Solution
In 0.10 M ascorbic acid, the equilibrim equation is
| C6H8O6 |
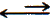 |
H+ |
+ C6H7O6- |
| 0.10 - x |
|
x |
x
|
The Ka for this equilibrium is
| Ka = |
[H+][C6H7O6-]
[C6H8O6]
|
= 8.0x10-5 |
Let [H+] = x; then [C6H7O6-] also equals x and
[C6H8O6] = 0.10 - x
Substituting these values into the expression for the acid dissociation
constant gives:
|
(x)(x)
0.10 - x |
= 8.0x10-5 |
Assuming, as before that [H+] is so much less than 0.10 M as to be insignificant
we rewrite the equation as
solving for x, we get:
x2 = 8.0x10-6
x = 2.8x10-3
Thus, in 0.10 M ascorbic acid, [H+] = 2.8x10-3 M.
|
C. Changing the Hydrogen Ion Concentration
in Solutions of Weak Acids; The Common-Ion Effect
We know that the solution of a weak acid contains the equilibrium
HA 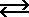 H+
+ A-
H+
+ A-
and, as long as the equilibrium exists, everything is in balance so that
If a substance is added to the solution that changes one of the concentrations,
the system goes out of equilibrium. Then either more molecules dissociate or
more ions combine until concentrations again fit the equilibrium constant expression.
When this set of concentrations is established, an equilibrium is again present,
the opposing rates are equal, and the concentrations become constant.
It is possible to calculate the new equilibrium concentrations after a change
in one concentration. Suppose we have one liter of a solution containing one
mole of acetic acid and one mole of sodium acetate. The acetic acid is present
as an equilibrium mixture if acetic acid molecules, hydrogen ions, and acetate
ions. The sodium acetate is present only as ions (recall from Chapter
7, Section 7.5C, that salts are completely ionized in solution). The acetate
ions from both the acetic acid and the sodium acetate participate in the acetic
acid equilibrium:
HC2H3O2 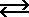 H+ + C2H3O2- Ka
= 1.8 X 10-5
H+ + C2H3O2- Ka
= 1.8 X 10-5
Although sodium ions are also present in solution, they do not participate
in the equilibrium, they do not appear in the equation for the equilibrium,
and they play no role in determining the concentrations of those substances
whose formulas do appear in the equilibrium expression. To calculate the hydrogen
ion concentration in this solution, we begin as in previous problems when only
the weak acid was present. If x equals the concentration of ionized acetic acid
molecules, the concentrations at equilibrium are:
| 1.0 - x = |
the concentration of un-ionized acetic acid molecules |
| x = |
the concentration of hydrogen ions |
| 1.0 + x = |
the concentration of acetate ions (the concentration of
sodium acetate in the solution plus the acetate ions from the ionization
of acetic acid) |
In the equilibrium equation, the concentrations are:
| |
HC2H3O2
1.0 - x |
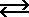
|
H+
x |
+
|
C2H3O2-
1.0 + x |
As in the case of a solution containing only acetic acid, we predict that
the concentration of ionized acetic acid, and therefore of hydrogen ions, is
very small and not significant when added to or subtracted from 1.0 M. Given
this assumption, 1.0 + x is approximately equal to 1.0, and 1.0 - x is also
approximately equal to 1.0. Thus, the concentrations can be expressed as
| |
HC2H3O2
1.0 |
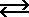
|
H+
x |
+
|
C2H3O2-
1.0 |
Substituting these values into the expression for the acid dissociation constant
for acetic acid and solving gives:
| |
Ka = |
[H+][C2H3O2-]
[C2H3O2] |
= |
(x)(1.0)
(1.0) |
= 1.8 X 10-5 |
| x = |
1.8 X 10-5 |
| [H+] = |
1.8 X 10-5 M |
The addition of sodium acetate has decreased the hydrogen ion concentration
from 4.2 X 10-3 M in 0.1 M acetic acid solution to 1.8 X 10-5
M in a 1.0 M acetic acid solution that is also 1.0 M in acetate ion. This decrease
is tremendous.
These calculations have shown that an ionic equilibrium such as the ionization
of a weak acid can be shifted by the addition of another ionic substance (such
as salt) that contains one of the ions present in the equilibrium. This effect
is known as the common-ion effect because it is
caused by the addition of an ion common to both substances.
|
Example:
Calculate the hydrogen ion concentration of a solution that is 1.0 M
in acetic acd and 0.20 M in sodium acetate.
Solution
If we let x equal the moles of acetic acid that ionize, the concentration
at equilibrium will be:
x = hydrogen ion concentration
1.0 -x = acetic acid concentration
0.20 - x = acetate ion concentration
We can drop x from the concentration of acetic acid and acetate ions
because, as has been shown before, x is not significant when added to
or subtracted from a number as large as 1.0 M or 0.20 M. The equilibrium
concentrations become:
| HC2H3O2 |
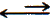 |
H+ |
+ C2H3O2- |
|
1.0
|
|
x |
0.20
|
Substituting these values into the expression for the acid dissociation
constant gives:
| Ka = |
[H+][C2H3O2-]
[HC2H3O2] |
= |
(x)(0.20)
1.0
|
= 1.8x10-5 |
or
0.20x = 1.8x10-5
x = 9.0x10-5
A solution that is 1.0 M in acetic acid and 0.20 M in sodium acetate
has a hydrogen ion concentration of 9.0x10-5 M.
|
H+ +
Cl-