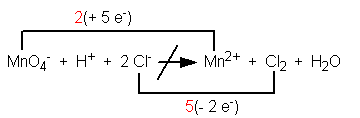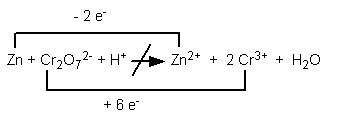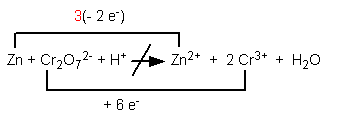The equations for some redox (a term meaning oxidation-reduction) reactions can be balanced by inspection as we have balanced all equations thus far in this text. However, many redox reactions have equations much too complex to be balanced by inspection without a great deal of frustrating trial and error. Such complex equations can more easily be balanced in a series of steps that utilize either (1) the changes in oxidation numbers of (2) the half-reactions involved. In both methods we will use ionic equations rather than complete formulas.

A. Balancing Redox Equations Using Oxidation Numbers
This method of writing balanced equations for redox reactions depends on knowing how oxidation numbers change during the reaction. Each step will be illustrated by developing the equation for the reaction of copper metal with nitric acid to form copper(II) ion and nitrogen dioxide.

Step 1. Write a skeletal equation for the reaction using the formulas of all ions, molecules, and atoms participating in the reaction. Example:

Step 2. If the reaction occurs in acid, add hydrogen ion and water as reactants or products. If the reaction occurs in base, add hydroxide ion and water as reactants or products. Example: this reaction takes place in acid. We will leave H+ as a reactant and add water as a product, knowing we might need H+ as a product or water as a reactant.

Step 3. Assign an oxidation number to each element in the skeletal equation. Example:

Step 4. For those elements that change oxidation number, use a line above or below the equation to connect the reactant form with the product form. Write above or below the line the loss or gain of electrons that accompanies the change. Example:

Step 5. Using multipliers, equate the loss and gain of electrons. Example:

Step 6. Multiply the coefficient of the substance oxidized or reduced by the multiplier used to equate the electron changes. Example:

Balance the oxygen by changing the number of water molecules present. Balance the hydrogen ions to match the water molecules. Example: Each nitrate ion yields one NO₂ and one O^2-. Two nitrate ions yield two O^2-. These require four hydrogens to form two water molecules, so the coefficient of H⁺ is changed to 4. The equation should now be balanced.

Step 7. Check that the charge is balanced. Example: the charge on the left is +2; the charge on the right is also +2. The equation is balanced.

Example: Potassium permanganate reacts with hydrochloric acid to produce manganese(II) ion and free chlorene. Write the balanced equation for the reaction using oxidation numbers. Solution Step1. The skeletal equation for the reaction is written below. Because the product chlorine is diatomic, a multiple of two chlorine atoms must be used in the equation. We prepare for this requirement by using 2 Cl- as a reactant. MnO4- + 2 Cl- Mn2+ + Cl2 Step 2. The reaction takes place in acid; add H+ as a reactant and water as a product. MnO4- + H+ + 2 Cl- Mn2+ + Cl2 + H2O Step 3. The oxidation numbers are: MnO4- + H+ + 2 Cl- Mn2+ + Cl2 + H2O +7, -2 +1  -1    +2  0 +1, -2 Step 4. Connect the two forms of the substances that change oxidation number and show electron change. Step 5. Equate the loss and gain of electrons. Step 6. Multiply the coefficients of the substances oxidized or reduced by the multipliers used to equate the electron change. 2 MnO4- + H+ + 10 Cl- 2 Mn2+ + 5 Cl2 + H2O Balance the oxygen and hydrogen using water and H+. We have 8 oxygens on the left; we need 8 water molecules on the right. This change will require 16 H+ on the left. Inserting these numbers gives the balanced equation. 2 MnO4- + 16 H+ + 10 Cl- 2 Mn2+ + 5 Cl2 + 8 H2O Step 7. Check that the charges are balanced. If they are, the equation is probably balanced too. On the left, -2 + 16 -10 = 4; on the right +4. The equation is balanced.

Example: Using oxidtion numbers, write the balanced ionic equation for the reaction of metalliz zinc with acidified potassium dichromate solution to yield zinc(II) and chromium(III) ions. Solution Step1. Write the skeletal equation for the reaction. Zn + Cr2O72- + H+ Zn2+ + Cr3+ Step 2. The reaction takes place in acid, so add H+ and H2O as needed. At the same time, note that the dichromate ion has two chromium atoms, so we will need a multiple of two chromium atoms in the product. To meet this requirement, put the coefficient 2 in front of the chromium(III) ion. Zn + Cr2O72- + H+ Zn2+ + 2 Cr3+ + H2O   Step 3. Assign oxidation numbers Zn + Cr2O72- + H+ Zn2+ + 2 Cr3+ + H2O 0 +6, -2  +1    +2    +3 +1, -2 Step 4. Connect the two forms of the substances that change oxidation number and show electron change. Step 5. Using multipliers, equate the loss and gain of electrons. Step 6. Multiply the coefficients of the oxidized and reduced substances in the equation by the same number used to balance the electrons. Balance the oxygen and hydrogen using waer and hydrogen ions. There are 7 oxygen n the left; we will need 7 water molecules on the right, which will require 14 hydrogen ions on the left. 3 Zn + Cr2O72- + 14 H+ 3 Zn2+ + 2 Cr3+ + 7 H2O Step 7. Check that the charges are balanced. On the left, 0 -2 -14 =12; on the right, 3(+2) + 2(+3) = 12. The charges are balanced; the equation is balanced.

B. Balancing Redox Equations Using Half-Reactions

The equations for oxidation-reduction reactions can also be balanced using half-reactions. Again we will illustrate this method using the reaction of nitric acid with copper metal to form nitrogen dioxide and copper(II) ion. The steps using this method are as follows:

Step 1. Write the skeletal equation for the reaction using the ions, atoms, and molecules that participate in the reaction. Example:

Cu + H⁺ + NO₃^- Cu²⁺ + NO₂

Step 2. Isolate the product and reactant form of each substance except H+ that occurs in the skeletal equation. Example:

Cu Cu^{2+
NO₃- NO₂}

Step 3. Balance these half-reactions by mass using hydrogen ions and water in acid solutions and hydroxide ions and base in basic solutions. Example:

^{Cu Cu2+
2 H+ + NO₃- NO₂ + H₂O}

Step 4. Balance the charges in these half-reactions using electrons as reactants or products. Remember that electrons are negative; they must be added to the more positive side of the equation. Example:

^{Cu Cu2+ + 2 e-
2 H+ + NO₃- + e- NO₂ + H₂O}

Step 5. Using multipliers, equate the numbers of electrons in the half-reactions. Example:

^{Cu Cu2+ + 2 e-
2(2 H+ + NO₃- + e- NO₂ + H₂O)}

Step 6. Add the multiplied half-reactions. Delete the electrons from both sides of the equation. Example:

Step 7. Check that the equation is balanced by mass and by charge. This equation has on the left 4(+1) + 2(-1) = +2; on the right, +2. The equation is balanced. Notice that, in this method, it is not necessary to determine the oxidation numbers of the various elements present.

Example: Using half-reactions, write the balanced equation for the reaction of sulfuric acid with iodide ion to form free iodine and hydrogen sulfide gas. Solution Step1. Write the skeletal equation for the reaction. H+ + SO42- + I- H2S + I2 Note that hydrogen sulfide is in the gaseous state; it is therefore not ionic and is written as a molecule. Step 2. Isolate the half-reactions.. H+ + SO42- H2S I- I2   Step 3. Balance these half-reactions by mass using hydrogen ions and water. 10 H+ + SO42- H2S + 4 H2O We have 4 oxygen atoms on the left, so we add 4 H2O on the right. They will require 8 hydrogen atoms. The hydrogen sulfide requires 2 hydrogen atoms. Together we need 10 hydrogen ions on the left. The second equation requires only a change of coefficient on the left. 2 I- I2 Step 4. Balance these half-reactions by charge by adding electrons to the more positive side. 10 H+ + SO42- + 8 e- H2S + 4 H2O 2 I- I2 + 2 e- Step 5. Equate the electrons in these half-reactions using multipliers. 10 H+ + SO42- + 8 e- H2S + 4 H2O 4(2 I- I2 + 2 e-) Step 6. Add the multiplied half-reactions. Delete the electrons. 10 H+ + SO42- + 8e- + 8 I- H2S + 4 H2O + 4 I2 + 8 e- Step 7. Check that the charges are balanced. On the left this equation has 10 + (-2) + 8(-1) = 0; on the right, 0. The charges are balanced; the equation is balanced.

Example: The reaction of permanganate ion, MnO4-, with oxalate ion, C2O42-, in acid solution forms manganese(II) ion and carbon dioxide. Using half-reactions, write the balanced equation for this reaction. Solution Step1. Write the skeletal equation for the reaction. MnO4- + H+ + C2O42- Mn2+ + CO2 Step 2. Isolate the half-reactions.. MnO4- Mn2+ C2O42- CO2 Step 3. Balance these half-reactions by mass. MnO4- + 8H+ Mn2+ + 4 H2O C2O42- 2 CO2 Step 4. Balance these half-reactions by charge by adding electrons to the more positive side. MnO4- + 8 H+ + 5 e- Mn2+ + 4 H2O C2O42- 2 CO2 + 2 e- Step 5. Equate the electrons in these half-reactions using multipliers. 2(MnO4- + 8 H+ + 5 e- Mn2+ + 4 H2O) 5(C2O42- 2 CO2 + 2 e- ) Step 6. Add the multiplied half-reactions. Delete the electrons. 2MnO4- + 16 H+ + 10 e- + 5 C2O42-               3 Mn2+ + 8 H2O + 10 CO2 + 10 e- Step 7. Check that the equation is balanced by checking the total charge on each side of the equation: on the left, 2(-1) + 16 + 5(-2) = +5; on the right, 2(+2) = +4.

Back   Home   Next