Free Energy and Equilibrium

A negative value of DG implies that a reaction is product-favored, i.e., after the reaction is completed there are more products than reactants. Conversely, a positive value of DG implies that a reaction is reactant-favored, i.e., after the reaction is completed there are more reactants than products.

In the Equilibrium Tutorial, the equilibrium constant, K, was discussed, which related the amounts of products and reactants of a reaction at equilibrium. A large value of K implies larger amounts of products than reactants, while a small value of K implies larger amounts of reactants than products.

Since both DG and K predict the relative amounts of reactants and products after a reaction is over, you may be wondering if DG and K are somehow related to each other. This is indeed the case:

DGº = -RTlnK_th     (2)

where R is the gas constant (8.314 J/mol•K), T is the temperature in Kelvins, and K_th is the thermodynamics equilibrium constant (equal to K_c and related to K_p by an equation described in the Equilibrium Tutorial). Thus, if K_th > 1, lnK_th > 0 and the minus sign means that DGº < 0, implying a product-favored reaction. If DGº > 0, lnK_th < 0 and K_th < 1, implying a reactant-favored reaction, as discussed above.

In practice, equation (2) is used if either DGº or K_th are difficult to measure directly. For example, the reaction of hydrogen and oxygen gases to form water vapor:

2H₂(g) + O₂(g) 2H₂O()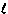

is so product-favored that it is impossible to measure the concentrations of hydrogen and oxygen gases to calculate K_th directly. Instead, DGº can be calculated from DG_fº values and the value of K_th can be calculated from equation (2).

Calculate the value of K_th for the reaction of hydrogen and oxygen.

K_th is so high for this reaction that if you put 4 kg of hydrogen gas and 64 kg of oxygen gas into a 1 cubic meter container and sparked the mixture, when the reaction was completed you would have 36 L of water, one molecule of oxygen and two molecules of hydrogen. These concentrations are impossible to measure, so K cannot be determined directly. It can be calculated using knowledge of thermodynamics.

Free Energy and Equilibrium